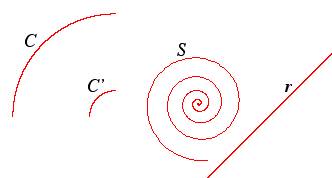
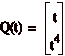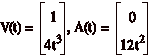Consideriamo gli archi C e C’ in fig. 2. Nei punti A e B gli archi hanno le stesse tangenti

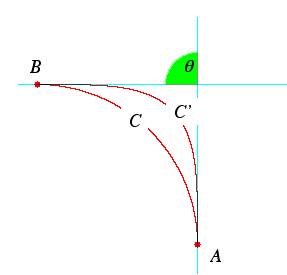
fig. 2

ed passando da A e B la tangente “gira” di un angolo q, ma la lunghezza di C è minore di quella di C’ (è evidente, anche se per provarlo sarebbe necessaria qualche accortezza) quindi in un certo senso C “impiega” meno percorso a girare di q e perciò è più curvo di C’. Possiamo formalizzare questa osservazione con la seguente

1 Definizione. Sia C una curva e A, B due suoi punti. La curvatura media dell’arco AB è

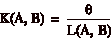
dove q è l’angolo formato dalle rette tangenti a C nei punti A e B e L(A, B) è la lunghezza dell’arco.

Con riferimento alla fig. 2, possiamo ora dire che la curvatura media dell’arco C è maggiore della curvatura media dell’arco C’.

2 Precisazione. In effetti le rette tangenti nei punti A e B formano ovviamente quattro angoli, dua a due uguali (cfr. fig. 3), tuttavia come mostra la successione di immagini

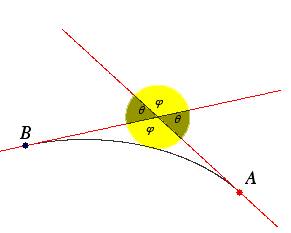
fig. 3

della fig. 4 (apri per vedere il filmato), l’angolo che misura come “gira” la tangente è solo

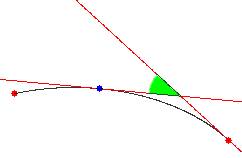
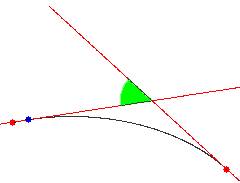
fig. 4* - Aprendo si vede un film del moto

uno dei quattro. Se poi invertiamo il verso di percorrenza, allora l’angolo che interessa è quello opposto, quindi uguale al precedente. Dunque non esiste nessuna ambiguità nella definizione.

Un’altra questione è la misura degli angoli. Conviene misurare gli angoli in radianti. Dire che un angolo misura q radianti, significa che presa una circonferenza di raggio 1 e centro nel vertice dell’angolo, l’arco di circonferenza che insiste sull’angolo è lungo q.

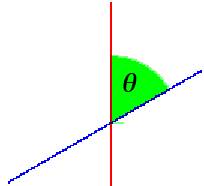
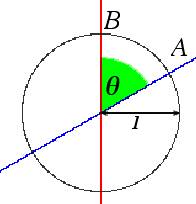
fig. 5 – Per stabilire quanto misura l’angolo verde a sinistra è necessario tracciare la circonferenza di raggio 1, a destra; risultato: q è la lunghezza dell’arco AB.

Poiché l’intera circonferenza è lunga 2π, un angolo piatto, che corrisponde ad una semicirconferenza è di π radianti, l’angolo retto (verde in fig. 6), che corrisponde a 1/4 di circonferenza è di π/2 radianti, quello celeste è di π/4 e quello giallo di 1 radiante (questo significa che l’arco su cui insiste è lungo quanto il raggio).

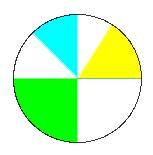
fig. 6

Anche se i matematici preferiscono non far uso di esplicite unità di misura, può essere utile dire che poiché la curvatura media è della forma angolo/lunghezza, essa si misura in radianti al metro oppure radianti al centrimentro. Ad esempio se la curvatura media è di π/2 radianti al metro, significa che percorrendo un’arco lungo un metro, la curva “gira” di un angolo retto.

3 Esempio. La curvatura media di un arco di circonferenza di raggio r è 1/r.

Calcoliamo la curvatura media di un arco di circonferenza di raggio r. Si osservi la fig. 5; poiché le tangenti in A e B sono perpendicolari rispettivamente ai raggi OA e OB, l’angolo q tra le tangenti è pari all’angolo tra i due raggi; l’arco AB è lungo L(A,B) = rq.

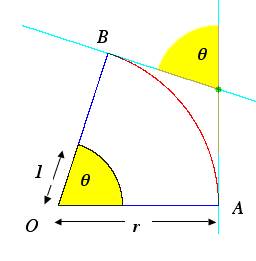
fig. 7

Quindi la curvatura è

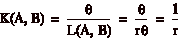
Dunque la curvatura media di una arco di circonferenza è il reciproco del raggio.

4 Esempio. Un segmento ha curvatura media nulla.

Infatti la tangente è diretta in ogni punto come il segmento e perciò q = 0. Ne segue che anche la curvatura è nulla.

Ritorniamo alla fig. 2: per gli archi C e C’, come abbiamo osservato K(C) > K(C’). Appare intuitivamente evidente che vicino agli estremi A e B l’arco C è più curvo, ma nella parte mediana il più curvo è C’. Dunque la curvatura media non sembra sufficiente a dar conto di tutti i fenomeni. Analogamente a quanto fatto per la velocità, introduciamo la seguente

5 Definizione. Dato un punto P di una curva, consideriamo la curvatura media di piccolo archi di curva che contengono P, il valore limite di tali curvature medie, al tendere della lunghezza di questi archi a zero, è – per definizione – la curvatura K(P) nel punto P.

Come vedremo non è un caso se usiamo la stessa lettera k che abbiamo usato per la curvatura con segno, l’unica differenza è che qui per distinguere le due usiamo la maiuscola.

La definizione di per sè non consente il calcolo se non in casi particolarissimi, vediamoli:

6 Esempio. La retta ha curvatura K nulla in ogni punto.

Infatti la curvatura media di ogni segmento è nulla.

7 Esempio. Tutti i punti di una circonferenza di raggio r hanno la stessa curvatura:

K = 1/r.

Infatti ogni archetto PQ ha curvatura media K(P,Q) = 1/r. Passando al limite, per Q che tende a P, resta ovviamente K(P) = 1/r.

Come vedremo queste sono le uniche curve piane con curvatura costante.

Per poter effettivamente calcolare la curvatura in altri casi intanto osserviamo che possiamo assumere che la curva sia la traiettoria percorsa da un punto mobile P(t) e limitarci a considerare la curvatura media di piccoli archi che hanno P(t) come estremo. Allora la curvatura in P(t) sarà

K(P(t)) = lim K(P(t),P(t+h))

h®0

Per calcolare la curvatura media K(P(t),P(t+h)) dell’archetto tra P(t) e P(t+h) conviene supporre che il moto si svolga a velocità 1. D’ora in poi useremo perciò il parametro s e la velocità sarà data dal versore T(s). Ciò significa che la lunghezza del percorso è pari all’intervallo temporale, che nel nostro caso è h; quindi se indichiamo con q l’angolo tra le tangenti nei punti P(s) e P(s+h), otteniamo semplicemente

K(P(s),P(s+h)) = q / h

Ora dalla fig. 8 a sinistra si vede che q è la lunghezza dell’arco T(s), T(s+h) perché sono vettori di lunghezza 1. Inoltre nella fig. 8 a destra sono confrontati sin q, la corda che ha lunghezza | T(s), T(s+h)| e l’arco.

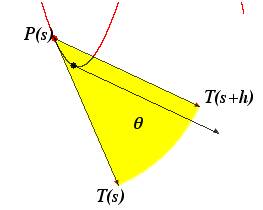
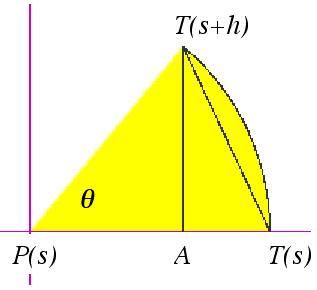
fig. 8 – Nella prima immagine il vettore T(s+h) compare due volte: applicato in P(s) e in P(s+h)

Dunque dalla figura:

sin q < |T(s+h) – T(s)| < q

Ma sappiamo che

lim sin q = 1

q®0 q

quindi anche

lim |T(s+h) –T(s)| = 1

q®0 q

E quindi per h piccolo possiamo considerare

K(P(s),P(s+h)) = q = |T(s+h) – T(s)|

h h

e troviamo finalmente:

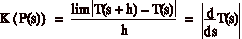
Ma ricordiamo chi era la funzione k(s) che compare nella formula di decomposizione dell’accelerazione:

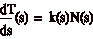
da cui segue (N è di lunghezza 1):

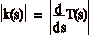
Confrontando otteniamo:

8 Teorema. La curvatura K in un punto è il valore assoluto della funzione k.

Naturalmente quando giriamo l’accelerazione è sempre diretta dalla parte della curva: se giriamo a sinistra il vettore accelerazione A è a sinistra della retta tangente, se giriamo a destra è a destra. Come sappiamo la componente normale dell’accelerazione è k v²N e N è sempre rivolto a sinistra della tangente. Qunidi k sarà positiva quando giriamo a sinistra e negativa quando giriamo a destra e in valore assoluto sempre uguale alla curvatura. E’ un buon motivo per chiamare k curvatura con segno.

In effetti se nella definizione di curvatura K avessimo tenuto conto della sinistra e della destra, cioè avessimo contato positivamente gli angoli corrispondenti alle curve a sinistra e negativamente quelli delle curve a destra, la definizione di curvatura K sarebbe coincisa con quella della funzione k.

La curvatura con segno ha un vantaggio indubbio: quando percorriamo una curva ad S cambia di segno e con questo ci avverte del fatto che siamo su una S. Ovviamente k si annulla nel punto della S in cui la curva cambia, perché è una funzione continua e sta cambiando di segno.

Si potrebbe pensare che una curva ad S possa essere riconosciuta con la sola curvatura, perché dopottutto anch’essa nel punto in cui la curva cambia si deve annullare. Ma consideriamo il seguente esempio.

Esempio. Consideriamo la curva

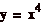
che è percorsa da

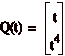
Risulta,

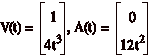
e dunque v(0) = |V(0)| = 1 e A(0) = 0. Allora anche la componente normale k(0)v(0)²N(0) = k(0)N(0) dell’accelerazione è nulla, perciò k(0) = 0. Guardiamo il grafico

è talmente piatto nel punto Q(0) che la curvatura è nulla, anche se non fa una S.

L’esempio dice che la curvatura (e quindi la curvatura con segno) si può annullare, anche se la curva non fa una S, questo mostra come la curvatura con segno sia indispensabile per riconoscere le S perché ce lo dice cambiando di segno.

Tuttavia la curvatura con segno ha un piccolo svantaggio teorico. Se percorro una circonferenza in senso antiorario, il versore normale è sempre diretto verso l’interno della circonferenza, come l’accelerazione; se invece mi muovo in senso orario il versore normale è esterno, mentre l’accelerazione e sempre diretta verso l’interno della curva. Dunque il segno della curvatura sarà positivo se vado in senso antiorario, negativo altrimenti. Questo dice che mentre la curvatura è una proprietà del punto della curva, la curvatura con segno dipende dalla scelta del verso di percorrenza (ecco perché abbiamo scritto K(P) per la curvatura e k(s) per la curvatura con segno)

Cerchio osculatore

Definizione. Dato un punto P sulla curva C, si prendano due punti Q ed R su C e si consideri l'unica circonferenza che per P,Q ed R (se non sono allineati). Quando Q ed R tendono a P, tale circonferenza converge al cerchio osculatore. Il raggio di tale circonferenza è il punto

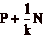
che è detto centro di curvatura. Il raggio è 1/k che è detto raggio di curvatura.

Dunque il centro di curvatura è il punto che si trova sulla normale alla curva nel punto P, a distanza pari al raggio di curvatura, dalla parte dell’accelerazione centripeta (concavità della curva). Se k nel punto P si annulla il raggo di curvatura diventa infinito.

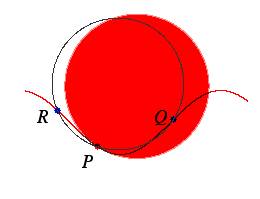
fig. 9* - In rosso il cerchio osculatore nel punto P; in nero la circonferenza che passa per i tre punti. E’ possibile muovere i punti Q ed R e vedere come cambia il cerchio osculatore al correre di P sulla curva.

Il nome osculatore deriva dal latino osculare = baciare, perché è la circonferenza che approssima meglio la curva vicino a P.

Vediamo alcuni esempi.

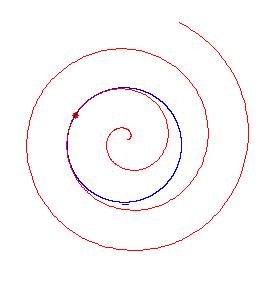
fig. 10* - Cerchio osculatore di una spirale

fig. 11* - Cerchio osculatore di un’ellisse

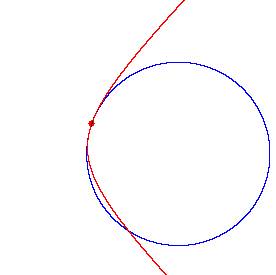
fig. 12* - Cerchio osculatore di un ramo d’iperbole

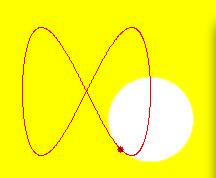
fig. 13* - Cerchio osculatore di una curva ad otto

Definizione. Data una curva, la sua evoluta è il luogo dei centri di curvatura dei suoi punti.

Esempi.

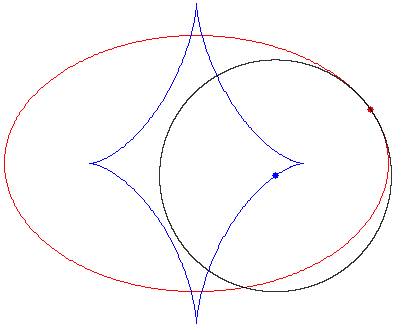
fig. 14* - Evoluta di un’ellisse

Teorema. La retta che congiunge un punto P di una curva, al centro C di curvatura è normale alla curva in P e tangente all’evoluta in C.

La prima affermazione è ovvia per come è definito il centro di curvatura. La seconda non la dimostriamo. Ma vediamo la seguente figura.

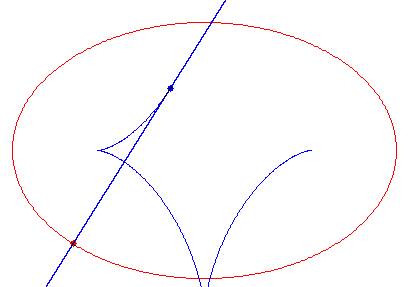
fig. 15* - Evoluta di un’ellisse con tangente.

Caratterizzazione delle curve mediante la curvatura

Sia data una curva C e un suo punto P. Fissiamo un verso di percorrenza sulla curva che percorriamo a velocità scalare 1. All’istante s saremo nel punto P(s) che viene dopo P se s > 0, prima di P se s < 0, e che abbiamo raggiunto dopo aver percorso un arco lungo |s|. Così il punto P(s) è individuato in modo univoco. E la curvatura con segno nel punto P(s) ha un preciso valore k(s). Dunque ho definito una funzione k(s).

Viceversa assegniamo una funzione k(s) qualsiasi e supponiamo (ma un istante vale un altro) che sia definita per s = 0. Fissiamo poi un punto P, una retta r che passa per P, e scegliamo un verso su r. Se ci muoviamo da P in direzione tangente ad r e nel verso fissato e a velocità 1, c’è modo di avere k(s) come curvatura? La risposta è sì e questo dice che la curvatura con segno definisce completamente la curva.

Per dimostrarlo ricordiamo che se conosciamo il vettore velocità e il punto iniziale (che nel nostro caso è P) allora la curva esiste ed è completamente determinata. Per altro noi sappiamo, la velocità è 1, che il nostro vettore velocità sarà un versore T(s) e quindi necessariamente della forma

T(s) = (cosq, sinq)

dove q è funzione di s. Allora il versore normale sarà

N(s) = (- sinq, cosq)

dT/ds = kN

Ma derivando

dT/ds = dq/ds (-sinq, cosq)

quindi per confronto

dq/ds = k

Dunque sappiamo che q è una primitiva di k. Inoltre all’istante 0 la tangente è nota (è la retta r, nel verso prescelto) cioè è noto q(0). Allora q è completamente determinata da k e quindi anche la traiettoria è completamente determinata.